
これいい本ですかねぇ…って思うんすよ。ちょっと実例を挙げて批判してみます。
簡単なテーブル作成の部分も腑に落ちない点が多いんですが、特におざなりなのが、相関解析の部分(p264~p273:散布図のビジネスへの応用)です。例えば、確かに本書のp268にはこう書いてある。
[散布図において…] 右肩下がりの場合も相関係数は正の数値となる。
これ間違ってねえですか?まず、ここらから始めてみて、本書の統計的にダメな部分・疑問な部分を考えていきます。例えば、生物科学研究所の井口豊先生もこうおっしゃってます。
決定係数に関しては,「決定係数は相関係数の二乗だから負(マイナス)にならない」と説明されることがある。しかしこの説明は,二点で明らかに間違いである。まず第一に,決定係数には複数の定義が存在し,必ずしも相関係数の二乗とはならない。第二に,負にならない定義の決定係数であっても,それは相関係数の二乗とは限らないのである。
決定係数R2の誤解:必ずしも相関の2乗という意味でなく,負にもなるし,非線形回帰には使えない
まず、R^2って正の値を前提とするものではない、ということが井口先生の研究室HPで上記のように解説されてて、そもそも相関係数って本書は言及してるけど決定係数と相関係数を混同しているような気がする。本書の執筆者は自由度修正済決定係数(モデルの正確さを表す)と単なる相関係数(二つの値の依存度を表す)の違いがわかっているのかな?
あと右肩上がりが相関係数+1って書いてあって、右肩下がりが相関係数-1って書いてあるけど、なんの前提条件もなしにして、相関係数を適当に取り扱っている気もします。これについては、池田信夫先生でさえかつてパラメータ調整なくして似たようなこと言ってた、という指摘もネット上でありますよね。ちょっとRで考えてみようかな、と。例えば次のコードを見てみてください。
|
1 2 3 4 5 |
test <- read.csv("相関解析検証.csv",header=TRUE) lmtest <- lm(売上~気温,data=test) plot(売上~気温,data=test) abline(lmtest) summary(lmtest) |
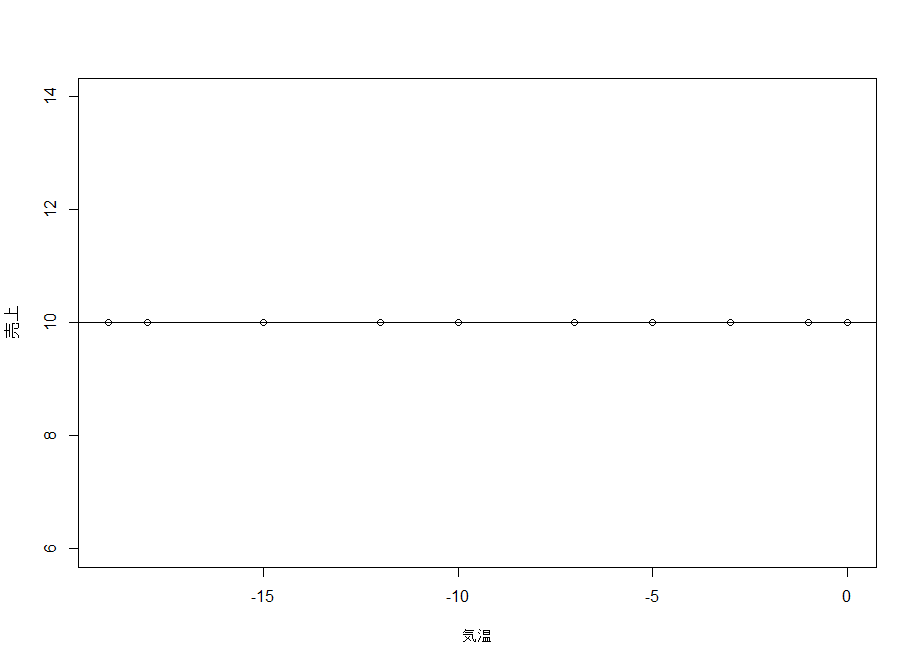
一番直観的に理解できて簡単なのがこの例だと思うんだけど。これ、観測点がマンマ水平に乗ってますけど、このとき決定係数R^2はどうなっているかっていうと…これまた上述のコード(summaryコマンドの部分)で出るんだよね。
Call:
lm(formula = 売上 ~ 気温, data = test)
Residuals:
Min 1Q Median 3Q Max
-1.203e-15 -6.477e-16 -3.702e-16 2.620e-17 6.651e-15
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.000e+01 7.991e-16 1.251e+16 <2e-16 ***
気温 -7.928e-17 7.481e-17 -1.060e+00 0.305
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.77e-15 on 16 degrees of freedom
Multiple R-squared: 0.5312, Adjusted R-squared: 0.5019
F-statistic: 18.13 on 1 and 16 DF, p-value: 0.0006011
ご覧の通り、正の値になってるけどねぇ。以下、p268より引用。
2つのデータのうち、一方の量や数値が増えると、もう一方の量や数値も増える場合、散布図のデータ分布は右肩上がりを示します。このような相関関係を「順相関」といいます。
いや、例えば、上のR出力図のように、気温にまったく左右されない売上を考えた場合(つまり、一方の量や数値が増えても減っても、もう一方の量や数値が一定のケース)でも「順相関」になってるよね?かたや、「順相関」の定義これ間違ってねえ?これは言葉のあやでもあるから、微妙なところだけど、アイスの売上を「順相関」として定型的に取り扱ったり、逆にカイロの売上を「逆相関」として定型的に取り扱ったりしていいのかしら?っても思います。
例えば、『アイスはアイスケースで保存していて、ケース外の売り場周囲の温度(アイスケース内の温度は一定と定義する)を気温として横軸に取り、かつ、徹底した社会共産主義の世の中であったとして、供給量が必ずいつ何時でも一定、需要がその供給をいつでも超えるケース(つまり、毎日供給分の上限まで必ず売り切れる社会体制)』を考えてみてほしい。⇑のようなプロットになるよね?あれ?これって「順相関」って言えんのか?そもそも順相関って相関係数が正の値をとることを言うんだよな?
シミュレーションの項目は微妙な本です。あくまでエクセルのノウハウを講じている書籍、として取り扱うべきであって、統計的なあやを紐解くようにできている書籍ではない。むしろ、そのようにしてとらえると、あまりに杜撰な点・間違いが多すぎると感じたのはあたしだけかしら,,,というわけで、本書を読むとしたら、松本氏の本と併読することをオヌヌメします!
※書影:Amazonより.


