ガラスタイプの分類：決定木分析

ガラスのタイプを様々な化学物質の関係上で分類したものを見る。今回は、mdaパッケージに含まれるデータファイルを活用する。今回使うソースコードが以下である。

install.packages("mda")
install.packages("rpart")
install.packages("rpart.plot")
library(mda)
library(rpart)
library(rpart.plot)

data(glass)
names(glass)
summary(glass)
hist(glass$Type)

glass.rp<-rpart(Type~.,data=glass)
glass.rp
rpart.plot(glass.rp,type=5,extra=101)

printcp(glass.rp)
plotcp(glass.rp)

#xerror+xstd（最終行）のこの合計がxであり...
#xがxerrorの各行の狭間に値する時その後列分のCPを見る。
#すると、CP=0.126445（分類木）であるので、prune内のcpをこれに指定する。

glass.rp2<-prune(glass.rp,cp=0.126445)
rpart.plot(glass.rp2,type=5,extra=101)

まず、ヒストグラムと初歩的な決定木分析の結果をみると…

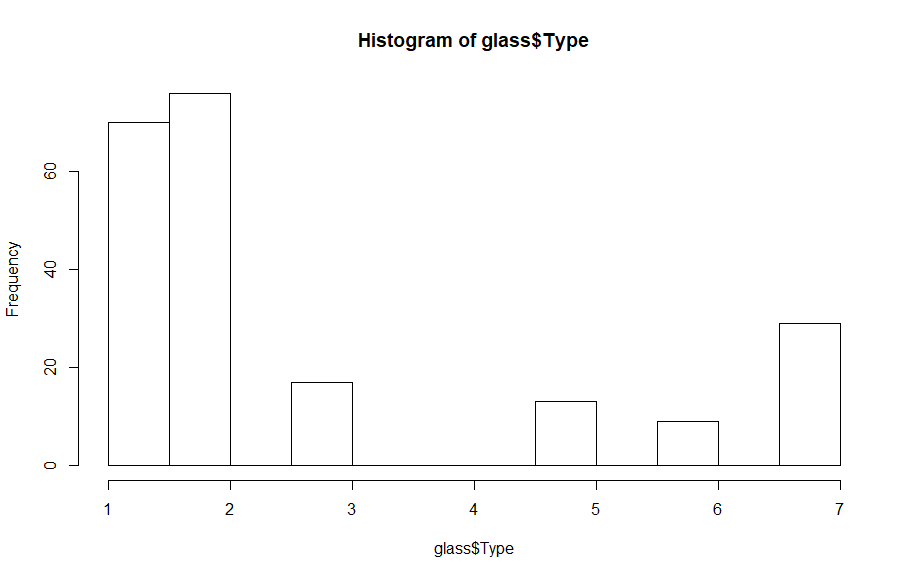
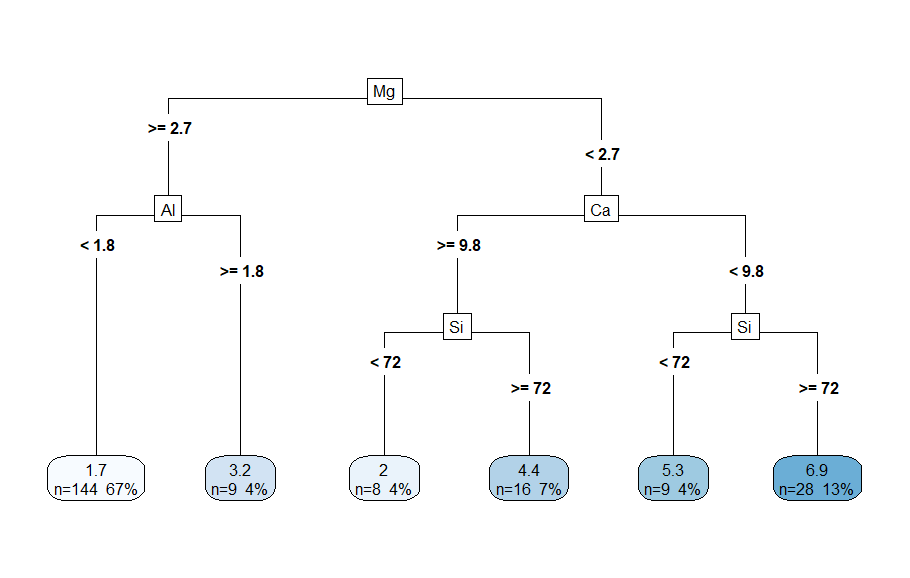
理想的な分布でガラスが生成されているのではないことがわかる（極性を持っている）。プロットしたものによれば、Mg量の値が強く分類し、Mg>=2.7のとき分派し、さらにAl量<1.8のとき、ガラスタイプ1~2に近しいものが一番多く生成される（67%）。ただし、ここでプロットされた木では計算量が多く効率的な判断ができないため、プルーニング（剪定）を行う。

Min+1SE法により、下記の部分で得られる表に基づき…

printcp(glass.rp)
plotcp(glass.rp)

xerror+xstdの合計xとするとき、このxがxerrorの各行の間を取る時において、その後列分のCP（複雑度：complexity parameter）を見ていく。Rにおける剪定コマンドprune内で、このCP=0.126445を指定する（その部位の剪定コマンドが最初に示したものと同じように次のコードとなる）。

glass.rp2<-prune(glass.rp,cp=0.126445)
rpart.plot(glass.rp2,type=5,extra=101)

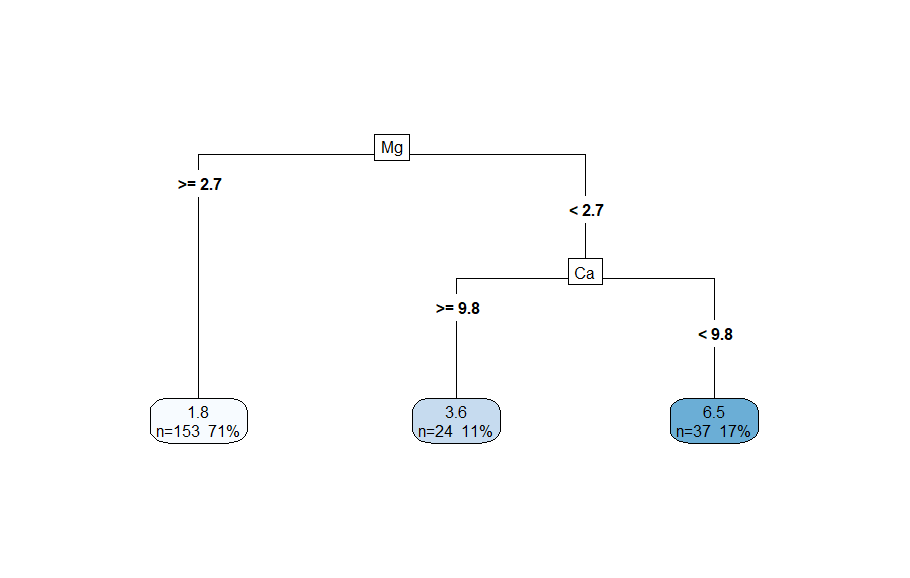
やはりMg量が強く関係し、これが>=2.7のときにガラスタイプ2よりのものが一番多くできる（71%）。そして、そのMg量でない時、次点でCa量が強く関係しこのCa量が>=9.8のとき、ガラスタイプ3~4のものが多くできる（11%）。ただし、このCa量でなかったときもガラスタイプ6~7のものがより多くできることがわかる（17%）。